基于设计健壮性的地磅秤台结构优化设计

健壮性设计是质量工程中一种重要的方法。从这个概念出发，基于产品健壮性设计理论，结合有限元分析和 优化设计技术，考虑多种工况，对地磅结构进行优化设计。

地磅产品是应用十分广泛的大型计量设备，主要由承重 的秤台体和传感器等测量系统两部分组成。其中秤台承受被 称物体的质量，占地磅总质量的主要部分。由于没有合适的 理论计算公式，秤台结构设计主要靠经验类比和简化计算，因 而无法对地磅产品钢结构进行优化设计。

通常经优化设计算法迭代得到的理论最优解，往往处于多 个约束边界上。如果产品受到内部或外部变异的影响,则该最 优点会发生偏移,甚至变成不可行解。讨论与有限元分析相结 合建立地磅秤台结构优化设计模型，根据产品健壮性设计理 论，考虑多种工况对秤台的U型钢的截面形状进行优化，既合 理有效利用材料,又保证设计的健壮性。

1.地磅结构分析和优化模型

1.1地磅秤台的结构形式、特点

以3mX 12 m/40 t双台面秤台为例，其秤台实际由两块3mX 6 m台面组合而成。每个台面仅由其四角支承在测量传感 器上，承受总工作载荷的一半。汽车停在秤台面上的位置是随 机的，设计时需要确定其典型的最不利工作位置。根据实际情 况确定汽车在秤台面上停放的不利位置是汽车刚驶上秤台或 停在台面中央。地磅形状和车轮荷载作用位置如图1所示.

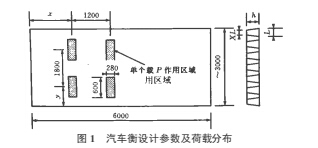
秤台结构由台面、U型钢和两端的端板组成，均为钢板制 作。U型钢共7根沿纵向布置对台面起加强筋的作用。端板 则保持台面横向刚度。根据设计要求选定的典型工作位置是: 纵向位置x = 140 mm和2 400 mm,以及横向位置= 130 mm 和600 mm,组合成总计4种工况。

1.2秤台结构的计算模型

整个地磅秤台有限元模型如图2所示。模型的详细情况。

（1）秤台由厚度不同的钢板组成。计算模型全部使用板壳 单元，共有42 806个节点,板壳单元数量43 764个，因此计算规模较大。

（2）地磅设计轴载为40t,因此，作用在一个台面上的载 荷为20 t设计时考虑动载荷系数B=1.3。

(3)在建立秤台的数学模型时，以U形钢的截面尺寸、端板 厚度作为设计变量，因这些变量对整个地磅的性能有较大的 影响。至于台面板厚度虽然对地磅强度和重量影响很大，但 其板厚的选取并非完全取决于其机械性能，因此，在这里仅作 为设计的给定参数。

(4)以秤台的质量G作为设计目标，以秤台的强度、刚度、 工艺要求和设计的健壮性作为约束条件,建立优化模型。

1.3优化的数学模型

优化设计问题可以描述为以下数学形式：

2.健壮性设计方法

大多数约束优化设计问题中，最优点都位于可行域的边界 上。这意味着设计参数只要出现很小的扰动，如在产品设计完 成进入制造和使用阶段时，由于制造技术、加工工艺、外载荷等 一系列不确定因素影响，可能会出现性能上大的变化，都可能 使最优点移动到可行域外,造成设计失效。为了避免这个问题, 必须使最优设计对设计变量的扰动不敏感。同样地，为了避免 最优目标函数值发生意外的变化，必须使目标函数在约束条件 下的敏感性最小。设计出对外部环境不敏感产品的过程称为健 壮性设计,使产品具有抵抗外界干扰所引起的功能波动的能 力,正是健壮性设计的目标。基于健壮性的产品开发方法，能够 同时或分别处理以下两种类型的问题：

使系统中的不可控因素y的变异，引起的系统性能变 异极小化；

使系统中的可控因素x的变异，引起的系统性能变异 极小化。

2.1 健壮性设计的主要途径

Pm-kinson将工程模型的健壮性分为两类：可行度健壮 性(确保设计约束即使在有变异的情况也能满足）和灵敏度健 壮性（减少设计对变异的灵敏度)，在任何一种设计中，都希望 能使设计达到其中的一种健壮性或两种都满足。在定量设计阶 段,设计者已经完成了概念设计，并已开发出工程模型。用优化 问题来表达定量设计问题,其数学模型为： 

Pm-kinson指出健壮设计的核心同样是一个优化问题,健壮 设计的一个关键概念是变量和参数的变异传递给了设计函数, 使目标和约束都产生变异。健壮设计的目的是减小所诱发的变 异。对于工程模型，采用较多的有下面六种健壮设计方法:

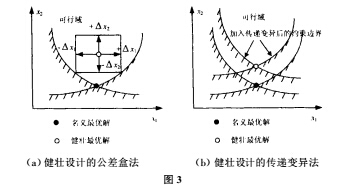
(1)公差盒方法（Tolerance Box Appioach)。

找到名义最优值后，对设计变量定义一个公差盒那么健 壮最优值是使公差盒位于可行域中时，离名义最优值最近的那 一点,见图3a其优点是使问题线性化在优化设计中容易操 作;但缺点是不能考虑不可控参数公差的影响，因公差盒仅仅定义在可行域内部。

（2）传递变异法(Method of Transmitted Variation)这种方法用一阶和二阶逼近式来估算传递变异所产生的 效果。然后考虑传递变异来修正名义设计以满足可行度健壮 性，或使传递变异最小化来实现灵敏度健壮性。该方法先从优 化问题中得出名义最优值（不考虑变异)，然后考虑传递变异进 行约束条件转换，可得可行度健壮性,见图3b。对于灵敏度健壮 性，需要在待求问题中加入对传递变异求极小值作为新的目标 函数。在求解优化问题过程中应用这种方法时，可以根据约束 的实际情况，向可行域内调整优化约束值，缩小优化模型的可 行域达到这一目的。

（3）优化后分析(Post Optimality Analysis ——POA)

对最优函数或变量求导数来研宄最优解对于象容差这样

小变化的响应。这种方法比起对问题的多次重新优化要有效得 多，尤其是想检查单个变量对多个参数的作用时。

（4）参数约束(Pa-ametric Constrains)。

目标函数中的一些参数受到一定范围的约束。对于最坏情 况的健壮最优解可由下列两种方法得到用一组约束来代替 参数约束,这些约束的和是参数约束；.把参数计算放入循环 中，用一个约束条件来确定范围。缺陷是同样仅适合于小容差 问题，且计算量大。

（5）随机优化。

实际问题中，很多参数并不确定，是随机分布的，满足一定 的分布函数。由此导出的目标函数和约束分布函数并非完全是 确定性的。随机优化的目的是求出满足可行性健壮性的最优 解，也就是满足特定的可靠性目标的最优解。

（6）田口方法。

是健壮设计方法中最著名的方法。利用正交表设计，对工 程模型进行试验，这样产生的新模型是一线性模型，用来在设 计空间内找到新的点来最小化、最大化或保持性能目标函数， 而同时使不可控制噪声最小化。

2.2基于灵敏度分析的健壮设计

灵敏度导数是指目标函数和设计变量对所研宄的参变量 的求导。Belegundu等研宄了通过极小化灵敏度来实现健壮 设计，即在设计阶段就通过选择适当的变量，使产品的质量对 不确定性因素的敏感性最小，使产品具有健壮性。基于灵敏度 分析的健壮性设计，可以称之为“狭义”的健壮性设计方法，主 要是利用灵敏度信息对优化以后的结果进行分析，使其具有健 壮性。在优化中考虑灵敏度，使约束条件对设计参数的灵敏度极小化。

计算目标函数和约束对参变量的导数,最直接方法是有限差分法。用一阶近似的前向差分格式表达导数的一般格式为：

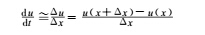
2.3健壮性设计的模型

根据前面分析，在健壮性设计中可有两种途径来考虑灵敏 度分析所起的作用:加入灵敏度分析产生的附加约束条件和加 入灵敏度分析产生的附加目标函数。

可以用下列方法施加基于灵敏度的约束:对灵敏度设置 上限;对灵敏度的最大值设置上限；对灵敏度的平方和设置约 束;对目标函数的灵敏度超过一特定值的概率加约束。

考虑到地磅结构分析工作量大，而优化设计模型本身却 较简单，可通过对灵敏度设置上限施加基于灵敏度的约束。

3.地磅秤台结构优化设计结果

根据前面所述方法完成对地磅的优化设计。优化前后 汽车衡u型钢尺寸及应力、位移情况汇总见表1。表中优化设 计的结果己经过圆整，此时优化模型中目标函数和主要约束的 灵敏度见表 2。

可见优化后结构的最大应力和位移虽都有所上升，但仍满 足设计约束，而且各工况下最大应力比较接近，说明钢材得到 了较充分的利用。优化后节省钢材约274 kg占原结构的6%。 另外从分过程知，汽车衡结构设计的主要控制条件是秤台面 的刚度要求。同时，设计得到的尺寸能使结构承受较大的内部 和外部变异的影响，而保持使用性能基本不变，使设计具有健 壮性。从灵敏度分析可以看出，目标函数和部分约束对端板厚 度变化敏感，互相制约。从优化计算的结果发现端板厚度变化 不明显，可以酌情处理为常量，这样可简化优化模型，加快寻找 最优点的速度。

4.结论

健壮性设计使设计在满足原有的目标函数的前提下，尽可 能使由于可控因素或不可控因素的变异造成系统的变异极小 化，这样得到的解能保证在系统受到内在因素或外界因素干扰 的情况下，仍能保持良好的性能。得到健壮性设计的解以后， 在后期的详细设计阶段对产品的参数在小范围调整时，不需要 或较少需要对系统的性能重新校验，节约了设计的时间和人力 资源。