称重原理—力矩平衡和静不定原理

称重原理—力矩平衡和静不定原理

本文详细分析了四支点静不定称重系统的工作原理以及角差修正和用于重心测量的问题，并举实例进行解读。

一、引言

本文所讨论的问题是重力式衡器称重遵循的两个基本原理：即衡器的静力平衡条件。物体保持静平衡的必要且充分条件是：诸作用力平衡∑（静力）=0 和诸作用力矩平衡∑（静力矩）=0。

另一个遵循的原理，即是静不定原理。一个有三个支点的物体，只要重心处于三支点构成的三角形内，物体始终处于稳定的静力平衡状态。并且根据支点和重心的几何位置，就可确定三个支点的受力大小，反之测得三个支点受力值，可确定物体的重量和物体重心的位置。从数学的角度讲，在这种情况，我们可以列出一个和力与两个力矩方程。根据这三个方程即可求出三个未知数，问题可精确求解。

对于有四个支点的物体，在理想的静平衡状态，只有在物体重心所处的三个支点组成的三角形的这三个支点才受力，而另一个支点是不会受力。然而在实际情况中，我们使用的器物往往都有四个支点。例如，将一个四条腿的凳子放在不平的地面，很可能只有三条腿着地，更甚者也可能只有两条腿支撑着摇晃的凳子，此时我们感到

在这两种情况下，凳子的状态并不稳定。但更多的情况是四条腿均着地，凳子处于稳定状态。这与理想状态相违背，在理想状态无论如何只可能有三支点受力，而现在四个支点都受力，造成这种情况的原因是由于地面不平所至。四个支点与地面的着力点不在同一水平面上。对于三支点的系统虽然着力点也不在同一水平面，但由静力平衡的条件可能得到一个和力方程与两个力矩平衡方程，由此可求解。而四支点系统也只能得到三个力学方程，不能求解。这样的系统称为静不定系统 （Statically Undefined Systems）。静不定问题在力学教材都有讲述。我们常见的四只传感器组成的衡器均为静不定系统。是本文讨论的主要问题。

二、衡器的静平衡

基于杠杆原理的杆秤、天秤，是最早使用的衡器，具有支点轴、载荷轴和力轴的简单杠杆，是最基本的衡器结构。每个轴的位置分别被称为支点、重心和力点。

按照这三个点的分布，可以把基本杠杆分为三种类型，即第一类杠杆、第二类杠杆和第三类杠杆，如图 1 所示。F 是支点、A 是重点、B 是支点，这三个力互相平行，它们作用力在同一直线上。

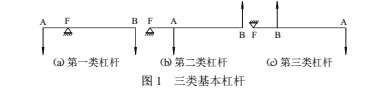
按照联接杠杆的数量可将杠杆 （系） 分为单一杠杆和复合杠杆 （系）。单一杠杆是独立的，如杠杆的杆和天平的横梁。而复合杠杆则是由相关联的杠杆组合而成，机械式的台秤和地秤均属复合杠杆结构。由四支传感器支承的电子衡器，四个支点、同时也是力点。承载器为框架结构的“二维杠杆”组成的复合杠杆系。

以第一类杠杆为例，分析其静力平衡和称重原理。在实际中，支点、重点和力点不可能在同一水平线上，如图 2 所示。

物的重量。

下面再讨论此类杠杆的“灵敏度”和“稳定性”。假设在重点 A 施加一小荷载△W，杠杆将产生一个小的偏转角△θ，杠杆达到一个新的平衡位置，根据图 2，此时杠杆在施加载荷后的力矩平

由此关系式可以得到以下结论：

（1） 若 ha≠0 或 hb≠0，S 受 W 或 F 的影响；（2） 若 ha=hb=0，S 不受 W 或 F 的影响；（3） 若 ha=hb=hc，则 S=∞，无穷大；（4） 若上式分母为负，则系统不稳定。

由于此结果的影响，在很长一段时间，人们认为把天平的负载荷盘置于天平横梁之上是不可能实现。直到 1670 罗伯威尔 （Roberval） 首先解决了这个问题，然而遗憾的是，还继续了近两个世纪，他的发明才获得应用。值得提出的是：罗伯威尔天平的另一个特点是称重结果与砝码和载荷放置的位置无关，即被测物体的重心处于承载器的不同位置其测量结果相同。

下面我们从数学的观点，讨论三支点衡器，如图 3 所示，A、B、C 三点放置传感器，被测物 W 重心到三边的距离为 ha、hb 和 hc。Ha、Hb 和 Hc 为三角形的高。根据力矩平衡条件：

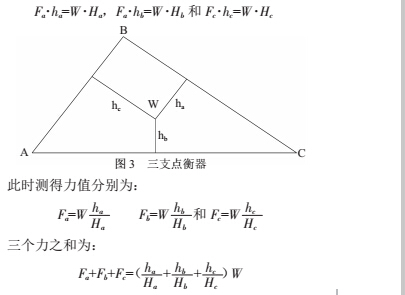
F·aha=W·Ha，F·ahb=W·Hb 和 F·chc=W·Hc

几何学证明：

ha  + ha  + ha  =1

Ha Ha Ha

即：Fa+Fb+Fc=W 与和力平衡方程一致。对于三支点衡器，通过测量三支点的力值就可得到被测物的重量的重心位置。反之，由被测物的几何位置和重量，通过计算就可求得三支点的受力大小。

三、静不定衡器

由四只传感器支撑的衡器，属于静不定系统。如前所述对于这样的系统，可得到一个和力方程与两个力矩平衡方程，而有四个未知数。因不能通过计算求出四只传感器的受力情况，如图 4 所

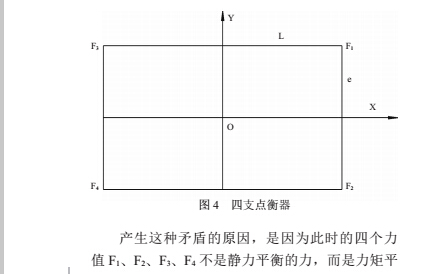
示。反之是否测得四只传感器的受力大小，就可得到被称物的重量？

在调四角偏载时得到四组数据，而且四组测量结果都不相同，可用下式表示：

F11+F21+F31+F41=M1

F12+F22+F32+F42=M2

F13+F23+F33+F43=M3

F14+F24+F34+F44=M4

这是与直觉很不一样的结果，同一重物由于放置位置不同测出不同的重量，而用来测量的四只传感器事先选用灵敏度相同的，按“道理”，测量结果应该是相同的。这种矛盾应如何解释？通常我们是通过一些大家认同的方法经调节后使四角偏载称重结果相同，却很少有人去思考矛盾发生的原因和调节方法的依据。

由此可见，此时测得的四个支点受力之和，

不等于被支撑物的重量。结果不仅与力矩平衡的受力分配系数有关，还与被支撑物的重心位置 X0

和 Y0 有关。还要特别记住，即使被支撑物的物理和几何状态没有变化，只要重心位置发生改变，力矩平衡的受力分配系数也发生改变。

根据上述分析，我们得到一个重要的结论，

对于静力平衡的第一个条件，即各作用力之和为零，这只有对共点力的情况成立，此时作用力的合力与诸反作用的合力相等。第二种静力平衡为力矩平衡，此时作用力与反作用力互为平行力，此时作用力矩等于反作用力矩。对于静不定系统，作用在四支承点力值之和不等于力矩的力值之和，

（7） 式的数学表示式就表明此种力学现象。使这

两个力值相等的必要而充分条件为：

K +K +K +K =4 和 （K +K）=（K +K） （8）

1 2 3 4 1 3 2 4

当此条件满足时，四支点的静不定衡器，用

来称重时，称重结果与被称物放置的位置，即重心所处位置无关，且四个支承点的力值之和就等于物体重量。这是对一台合格的衡器的基本要求。所以 （8） 式是我们对角偏载调节的理论根据。

四、偏载调节

一台不经偏载调节合格的秤，是不可能称为合格的衡器。偏载调节有很多方法。下面介绍一种对四支点衡器的偏载调节方法。

众所周知，使用模拟传感器的汽车衡，通常是将传感器并联使用，并事先将传感器的灵敏度配对，配对的要求一般选择四只传感器灵敏度间偏差在千分之一以内，最好将输出阻抗也选择一致，输出零点也在指标之内。然而，即使这样，四角偏差通常也超过规程要求。为了调节角差，是通过改变传感器的供桥电压或输出阻抗，改变原来的灵敏度使角差调至一致。此时传感器的实际“灵敏度”可能明显的超过原来配对的一致性。由于四只传感器相互并联，彼此互为负载，当改变桥压和输出阻抗时，都会对其它传感器的工作状态发生影响，这种角偏调节是很麻烦和费时的工作。调节的“标准”是试图将传感器现实的输出调至相同，或根据计算将四只输出电流调至一致。

对数字传感器或数字通道的汽车衡的角差调节。使用的方法简单、直观。将四角测出偏差值，通过软件手段将其调为相同。

下面介绍我们的方法，未经修正前的实测数据如表 1 所示。

最终的测量结果，是将此时四只传感器测得的力值相加。在此要特别注意：这些力值是力矩平衡的数值，而不是静力平衡的数值。

一台合格的衡器要求称重结果与被称物放置的位置，即重心的位置无关。调角差的目的就在于此。下面给出了角差测量值的数学表示式：

K11M0+K21M+K31M0+K41M0=M1

K12M0+K22M0+K32M0+K42M0=M2

K13M0+K23M0+K33M0+K43M0=M3

K14M0+K24M0+K34M0+K44M0=M4

我们的角差修正值是根据上式，用修正前的数据解此方程，对系数 K 修正，结果如表 2 所示。

表 2

修正后的结果如表 3 所示，修正前测量结果平均值为 87908.3，与均值的最大偏差为 0.3%左

右。修正后测量结果的平均值为 87908.5，此时与平均值的最大偏差小于万分之一。

无论何种修正，最终还必须经实测验证。

五、重心测量

利用称重方法测量物体的重心，是一种简便、实用的方法。在上世纪九十年代我与哈工大的老师研制过一台测量坦克重心的装置，近些年参与一些重心测量的项目。本文是在重心测量工作中涉及的一些问题的启发而写的。

根据力学原理，力矩平衡点即是物体的重心点。一个系统的支点就是系统的重点。系统将保持平衡。对于静不定系统的四支点衡器，此时在 y

方向的力矩平衡方程为：

F1+F3=（1+y/e）M/2 F1+F3=（1+y/e）M/2 和 M=F1+F2+F3+F4

上两式相减可得到在 y 方向力矩平衡的坐标位

置：

y/e=[（F +F）-（F +F）]/（F +F +F +F） （9）

1 3 2 4 1 2 3 4

而根据 （3） 和 （4） 有以下关系：

此时由四只传感器测得的力值，求得的力矩平衡点不与物体的重心位置相重合。只有在满足（8） 的条件下，测得的力矩平衡点才是被测物的重心。修正前和修正后的数据计算得到的力矩平衡位置和力矩平衡的受力分配系数，如表 4、表 5

所示。在这里讲到计算 y 轴方向的结果。

分之一以内，可认为基本满足 （8） 的条件，求得的修正后的力矩平衡点的坐标值，就是角偏放置砝码的重心的位置 y0。各象限的砝码力矩平衡重心坐标 y0 值，就是按此结果，根据 （3） 和 （4） 式

求得。结合第二、第四象限和 X 轴方向的计算结果，可帮助更详细了解四支点衡器的受力情况。

六、问题与思考

（1） 在测角偏时，所测的四角的数值各不相同，有时测得结果还会大于使用砝码的值。这种矛盾你能解释吗？

（2） 有人认为：衡器中心位置就一定是测量最准确的位置。这种观点正确吗？在用比较法检定砝码时，应如何评价由两者位置偏离对误差的影响？

（3） 传统调偏将四角的输出调为一致。理论上依据是什么？如何估计这种方法的误差？

（4） 多于四个支点的衡器应如何调角差？

（5） 是否只用四只传感器省去承载器可用来称重或测量重心？

现实中由于不能理解四支承衡器静不定属性，而产生的误区较为常见，往往使得工作事倍功半或造成错误结果。

七、结束语

本文所讨论的问题，我在中、外衡器资料中没有发现有关文章。上述的分析和论述是我思考的结果，供有兴趣者讨论。